前回は PyTorch のチュートリアルの最初だけやってみた。そこで PyTroch の自動微分の概念が重要であることが分かったので、今回は自動微分のチュートリアルをやってみる。ページは以下。

忘れてはいけないのは PyTorch のテンソルはお化けオブジェクトであるということ。どんな情報を持っていてもおかしくない。そこに惑わされないように今回も気をつけよう。例によって、本記事で記載するソースコードや図は上記のチュートリアルからの引用である。

Automatic Differentiation

このチュートリアルは以下のプログラムについて扱っている。テンソルをたくさん作って計算している。

import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

重要なポイントは、このプログラムは単にテンソルの計算するだけでなく、計算グラフ（computation graph）を構築している点。以下のようなグラフが構築されると考えればよいらしい。

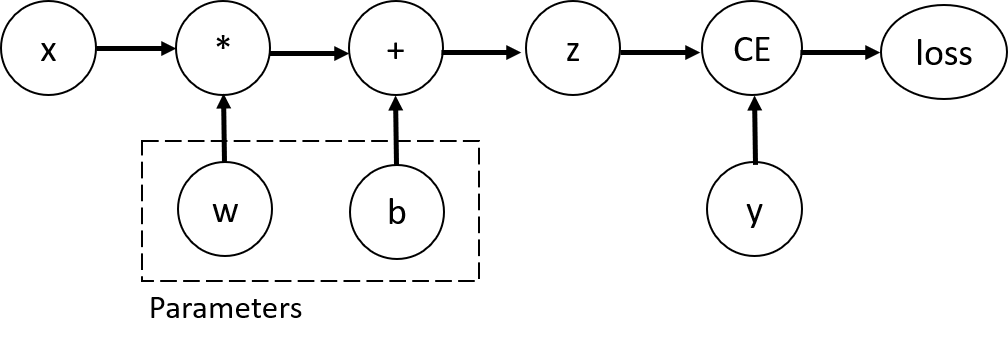
f:id:t-keita:20210904134426p:plain:w600

このグラフのノードがテンソルを表しており、エッジは各テンソルがどのテンソルをもとに計算されているのかを表している。もちろんテンソルに対する任意の演算が計算グラフ上で表現できるとは限らず、その演算が torch.autograd.Function クラスのインスタンスになっている必要がある。

図中の Parameters と書かれている部分は最適化の対象となるパラメータであり、プログラム中では requires_grad=True を指定することで表現される。ちなみに、バックプロパゲーションにより勾配計算が伝播されるので、実際はグラフのノード同士は単方向ではなく双方向につながっていることが予想される。

そして、最終的な誤差を計算グラフ上に伝播させることで各パラメータの勾配を求める。以下のコードで実行できる。

loss.backward()
print(w.grad)
print(b.grad)

当たり前だが、勾配が求まるのはパラメータだけであり、x などの学習データのテンソルの勾配が計算されるわけではない。パラメータは requires_grad=True が指定されたテンソルであり、この世界では特別な存在だと思ったほうがよさそう。

ここまでの話で、テンソルの計算をしていると見せかけて裏ではグラフが構築されることがわかった。PyMC3 とかの確率的プログラミングに似ている印象を受ける。確率的プログラミングでは確率変数の計算をプログラム上で記述すると、裏では対応するベイジアンネットワークが構築される。そんな感じ。

実験してみる

要するに、テンソル演算の偏微分をもとに勾配を計算できるわけだ。ってことで簡単な例を用いて実際に勾配を計算してみる。

ここでは2次関数の勾配を求めている。具体的には、2次関数 $y = x^2 + 1$ の $x = 3$ における傾きを求めてみる。あらかじめ手計算で答えを求めておくと、 $\frac{\partial y}{\partial x} = 2 x$ なので $x = 3$ における傾きは 6 である。

これを PyTorch のプログラムとして表現すると以下のようになる。

x = torch.Tensor([3])
x.requires_grad_(True)
y = x * x + 1
y.backward()

得られた x の勾配を見てみると、確かに 6 が得られていることが分かる。

print(x.grad)
# -> 
tensor([6.])

ニューラルネットワークというのは一種の計算グラフを表しているに過ぎない。勾配計算の逆伝播がニューラルネットワークの構成要素に対してできるようになっているので、PyTorch のユーザは部品を組み合わせてニューラルネットワークを定義するだけでパラメータの最適化を実行できるというわけである。

optimizer と loss はどう関係しているのか？

ここで前回の記事の疑問に戻ってくる。以下のようなプログラムでパラメータを更新できるのが気持ち悪いのであった。特に optimizer と loss の間のデータフローがよく分からなかった。

model = NeuralNetwork().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
...
        pred = model(X)
        loss = loss_fn(pred, y)
        # Backpropagation
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

今になってみるとそれなりに仕組みが分かるぞ。loss.backward() によって、 loss を求めるために必要な各テンソルの勾配が計算される。裏では計算グラフ上で勾配の伝播計算が走っていると思えばよさそう。model のパラメータとなるテンソルは裏では requires_grad=True になっているんだろう。そして optimizer はそれらのテンソルへの参照を保持している。そのため、loss.backward() で計算された勾配を使って optimizer がパラメータの更新を行えるという仕組みなんだろう。